^{Acides, bases
et pH - pH des acides et bases faibles seuls}

Accueil

Logiciels et bibliographie

Programme d'étude

Cours
Acides, bases et pH

Pour un acide faible seul

HA + H₂O

H₃O⁺ + A^-Co - x x x

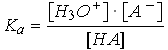En négligeant l'autoprotolyse de l'eau, on a [H₃O⁺] = x et K_a = x² / (Co - x)

Comme l'acide est faible, on fait l'approximation : C_o >> x donc (Co - x) 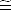C_o

On remplace et on obtient : K_a · C_o = x² = [H₃O⁺]²

D'où 2 · log ([H₃O⁺]) = log K_a + log C_o ce qui entraîne pH = 1/2 pK_a - 1/2 log C_o

Exemple :

Calculons le pH d'une solution de HCN 0,1 mol/L (pK_a = 9.4)

pH = 1/2 pK_a - 1/2 log C_o ce qui donne pH = 5,19

Attention: L'approximation faite, C_o >> x n'est plus très valable si Ka > 10^-3 donc pour des pKa < 3, il faut alors faire le calcul sans cette approximation.

Pour une base faible seule

A^- + H₂O

AH + OH^-Co - x x x

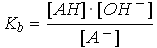En négligeant l'autoprotolyse de l'eau, on a [OH ^-] = x et K_b = x² / (Co - x)

Comme la base est faible, on fait l'approximation : C_o >> x donc (Co - x) 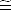C_o

Par remplacement dans la formule, on obtient :

K_b · C_o = [OH^-]² en remplaçant [OH^-] = K_e / [H₃O⁺] et K_b = K_e / K_a

On obtient Ke · C_o = Ka · (K_e / [H₃O⁺])² ce qui se simplifie: [H₃O⁺]² = Ka · Ke / C_o

D'où pH = 7 + 1/2 pK_a + 1/2 log C_o

Exemple:

Calculons le pH d'une solution de NH₃ 0,001 mol/L (pKa = 9.22)

pH = 7 + ½ · 9.22 + ½ · log(0.001) ce qui donne pH =10,11

Attention: L'approximation faite, C_o >> x n'est plus très valable si Kb > 10^-3 donc pour des pKb < 3, il faut alors faire le calcul sans cette approximation.

Limite des approximations

Pour que les formules soient valables, il faut que le degré de dissociation de l'espèce soit inférieur à 5 %. Par exemple, pour le calcul du pH de CH₃COOH 0.001M:

Avec la formule pH = 1/2 pK_a - 1/2 log C_o On obtient: pH = 2.38 + 1.5 = 3.88

Contrôle du degré de ionisation: -log [H₃O⁺] = 3.88 donc [H₃O⁺] = 1.318 · 10^-4

% de ionisation = ( 1.318 · 10^-4 / 0.001 ) · 100 = 13. 8 %

L'approximation n'est pas valable et il faut faire le raisonnement complet:

Espèces:	CH₃COOH	H₃O⁺	CH₃COO^-
Etape 1: Molarité initiale	0.001	0	0
Etape 2: Variation	- x	+ x	+ x
Etape 3: Molarité à l'équilibre	0.001 – x	x	x

Etape 4: Introduire dans la constante d'acidité:

Ka = 1.8 · 10^-5 = x² / (0.001 – x)

x² + 1.8 · 10^-5 x – 1.8 · 10^-6 = 0 Solution : 0.00012547 (et -0.00014347 à éliminer)

pH = - log x = 3.90 On voit que l'erreur est ici encore très faible ! (ce qui n'est plus du tout le cas avec des pKa proches de zéro)

Exercices

Exercice 1: Quel est le pH d'une solution aqueuse renfermant 3 g d'acide acétique (CH₃COOH, pK_a = 4,78) par litre ?

Exercice 2: Quel est le pH d'une solution aqueuse renfermant 1,38 g de nitrite de sodium (NaNO₂) par litre ? On connaît pK_a (HNO₂) = 3,3.

Exercice 3: Soit HNO₂ (pKa = 3,3) M/10, quel est le pH de cette solution ?

Exercice 4: Une solution de HNO₂ 0,2 M a un pH de 2,02. Quelle est la valeur de son Ka?

Exercice 5: Une solution de fluorure de potassium (KF) a un pH de 8, quelle est la concentration de KF (M et g/l) ? On connaît le pK_a (HF) = 3,2.

Exercice 6: Une solution d'acide hypochloreux (HClO, pK_a = 7,5) a un pH de 4,5. Quelle est la concentration de l'acide hypochloreux en M et en g/l ?

Exercice 7: Le pH d'une solution de HClO₂ 0.1 M est de 1.2. Quelles sont les valeurs du Ka et du pKa de l'acide chloreux?

Exercice 8: Calculer le pH des solutions suivantes:
a) HCOOH 0.2M (pKa = 3.75) b) NH₂NH₂ 0.12M (Hydrazine) (pKb = 5.77)
c) C₆H₅COOH 0.15M (pKa = 4.19) d) C₁₀H₁₄N₂ 0.0034M (la nicotine, une base) (pKb = 5.98)

Exercice 9: Le pH d'une solution de C₃H₇NH₂ 0.1 M est de 11.86. Quelles sont les valeurs du Kb et du pKb de la propylamine?

Exercice 10: On met 1 g de HIO₃ dans un litre d'eau, calculer le pH de trois manières :
a) Avec la formule des acides faibles.
b) En considérant que c'est un acide fort.
c) Sans faire l'approximation que la dissociation de l'acide est faible.

Acides, bases et pH - pH des acides et bases faibles seuls

^{Acides, bases
et pH - pH des acides et bases faibles seuls}