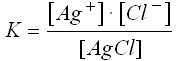 Equilibre
chimique - équilibre hétérogène
Equilibre
chimique - équilibre hétérogène
Logiciels et bibliographie
Programme d'étude
Cours
Equilibre chimique
- Définition
- Déplacement de l'équilibre
- Application: changements d'états
- Application: osmose
- Application: le phare halogène
- Raisons de l'existence d'un équilibre*
- Constante d'équilibre*
- Equilibre hétérogène, produit de solubilité*
- Exercices*
L'expression de K se simplifie lorsqu'il apparaît des corps solides ou liquides dans l'équation chimique.
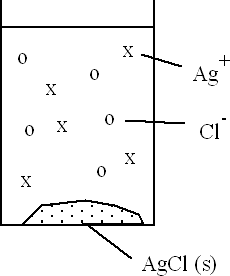
Par exemple quand on met un solide ionique dans l'eau en quantité plus grande que ce que le liquide peu dissoudre, on obtient une situation d'équilibre entre le solide et ses ions dissociés dans le liquide. Par exemple avec AgCl qui est un produit ionqiue très peu soluble dans l'eau:
 |
Un
équilibre s'établit entre AgCl solide et
ses ions: 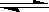 Ag+ +
Cl- Ag+ +
Cl-
Le dénominateur est une constante, on peut donc définir une nouvelle constante appelée produit de solubilité Ks : Ks = [Ag+] · [Cl -] Pour AgCl : Ks = 2,8 · 10-10 Ks est une constante à une température donnée. On peut trouver dans des tables les valeurs de Ks pour beaucoup de substances. |
Application: Calculons la solubilité en g/l de CaF2 dans de l'eau pure et dans une solution de Ca(NO3)2 0,1 M. Sachant que Ks (CaF2) = 1,7 . 10-10 .
Dans l'eau pure
CaF2
(s)
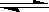 Ca2+ + 2F-
Ca2+ + 2F-
Ks
= [Ca2+]·[F-]2
= 1,7 .
10-10
(CaF2) = 78 u
[Ca2+]
= ?? [F-]
= ??
Posons que [Ca2+] = x ce qui implique que [F-] = 2x.
On a alors x .
(2x)2 = 1,7 . 10-10,
donc 4x3 = 1,7 .
10-10 d'où x = 3,5 . 10-4.
Dans une solution de Ca(NO3)2 0,1 M
Ca(NO3)2 est soluble et il y a ainsi déjà des ions Ca2+ en solution, la solubilité de CaF2 sera donc encore moins bonne que dans l'eau pure à cause de cet effet de "ion commun" qui déplace l'équilibre
CaF2
(s)
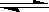 Ca2+ + 2F-
vers la
gauche (principe de Le Chatelier)
Ca2+ + 2F-
vers la
gauche (principe de Le Chatelier)
x
2x
Il s'agit aussi de calculer le
nombre de moles de CaF2
qui ont passé en solution, mais en présence d'ions Ca2+
déjà en solution !
[Ca2+] = 0,1 + x
et [F-]
= 2x
[Ca2+] ·
[F-]2 = 1,7 .
10-10 ce
qui donne une équation en x3.
Comme
x << 0,1, on peut négliger x pour la concentration de
Ca2+ (il
faudra vérifer que cette approximation est valable en fin de calcul en
s'assurant que x est inférieur au 5% de l'autre valeur, ici
0.1)
On a alors [Ca2+] = 0,1 et [F-]
= 2x
Ks = 0,1 . (2x)2
= 1,7 . 10-10 donc 0,4 x2
= 1,7
. 10-10
d'où x2 = 4,25 .
10-10 d'où x = 2,06 . 10-5.
Vérification de l'approximation: 2,06 . 10-5 / 0.1 = 2,06 . 10-4 < 0.05 donc l'approximation est valable.
La solubilité est donc de 2,06 . 10-5 . 78 = 1,6 . 10-3 g de CaF2/L
La solubilité dans cette solution est donc environ 10 fois plus faible que dans de l'eau pureExercice 1 : On mélange 50 ml de AgNO3 10-3 mol/L et 50 ml de K2CrO4 10-3 mol/L, y aura-t-il précipitation de Ag2CrO4 ? Ceci connaissant l'équilibre de précipitation (les autres sels sont solubles):
2AgNO3 +
K2CrO4 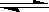 Ag2CrO4
Ag2CrO4 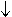 + 2KNO3
Ks( Ag2CrO4 ) =
5,32 . 10-1
+ 2KNO3
Ks( Ag2CrO4 ) =
5,32 . 10-1 
Exercice 2
: Quelle est la solubilité
(mol/L et en g/l) dans l'eau pure du CaSO4?
(Ks
(CaSO4)
= 6 .
10-5). 
Exercice 3
: Quelle est la solubilité
du CaSO4
dans une solution
contenant déjà une
concentration de CaCl2
de 10-2 mol/L ? On sait que CaCl2
est complètement dissocié. On connaît Ks
(CaSO4)
= 6 .
10-5. 
Exercice 4
: Quelle est la solubilité
du CaF2
(Ks(CaF2) = 3.9 .
10-11) dans une solution
contenant déjà :
a)
NaF 10-2 mol/L
b) CaCl2
10-3 mol/L 
Exercice 5
: Exprimer
la loi d’action de masse pour les équilibres suivants :
a) ZnO (s) + CO (g) 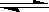 Zn (s) + CO2 (g)
Zn (s) + CO2 (g)
b) A (g) + B (s) 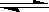 C
(s) + D (s)
C
(s) + D (s)
c) H2O 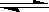 H+ + OH-
H+ + OH-
d) AgCI (s) 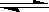 Ag+ + CI-
Ag+ + CI-
e) Zn (s) + 2 Ag+
(aq) 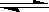 2 Ag (s) + Zn ++
(aq)
2 Ag (s) + Zn ++
(aq)
f) ZnO (s) + CO (g) 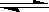 Zn (s) + CO2
(g)
Zn (s) + CO2
(g)